Introdução à sistemas de controle

Aviso

Esse material ainda está em uma versão preliminar. Sugiro uma leitura rápida para acompanhar a instrução, mas saiba que ele será revisado para que possa estudar melhor mais tarde.

A teoria de controle de sistemas trata da capacidade de influenciar o comportamento de sistemas dinâmicos através de comandos ou ações de controle. Sistemas dinâmicos são caracterizados por estados que variam com o tempo, e isso pode incluir sistemas mecânicos, elétricos, químicos, biológicos, entre outros. No contexto da engenharia, o objetivo principal é fazer com que um sistema siga uma determinada referência ou responda de uma maneira desejada a perturbações externas. Por exemplo, no controle de um drone, a teoria de controle pode ser usada para estabilizar o voo e permitir que o drone siga uma trajetória predeterminada.

O motivo pelo qual a teoria de controle é essencial decorre da complexidade encontrada em muitos sistemas dinâmicos. Sem um entendimento teórico sobre como os sistemas respondem a diferentes entradas e perturbações, seria extremamente difícil, senão impossível, desenvolver controladores que possam fazer o sistema se comportar de maneira desejada de forma confiável e segura. Além disso, a teoria de controle oferece ferramentas matemáticas para analisar a estabilidade, desempenho e robustez de um sistema controlado, o que é crucial para assegurar que o sistema não apresentará um comportamento indesejado ou perigoso em condições reais de operação.

Autoestudo

Sistemas de malha aberta

Sistemas de malha aberta são sistemas de controle nos quais a saída não é medida nem realimentada para ajustar o comportamento do sistema. Um exemplo clássico é um forno elétrico antigo, onde a entrada de controle é a tensão aplicada aos elementos de aquecimento. Nesse exemplo, suponha que você defina uma tensão específica com o objetivo de atingir uma certa temperatura no forno. No entanto, como o sistema é de malha aberta, ele não tem conhecimento da temperatura real dentro do forno. Além disso, há perturbações, como a troca de calor indesejada com o ambiente externo, que podem afetar a temperatura interna do forno. Como não há realimentação que ajuste a tensão em resposta a essas perturbações ou a diferenças entre a temperatura desejada e a real, o sistema de malha aberta pode ser impreciso e ineficiente em manter a temperatura desejada de maneira consistente. O diagrama de blocos do sistema em questão pode ser visto abaixo:

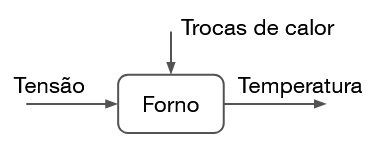
Funções de transferência

Autoestudo

Funções de transferência são uma ferramenta fundamental na teoria de controle de sistemas, que relacionam a saída de um sistema à sua entrada no domínio da frequência ou domínio complexo, geralmente usando a Transformada de Laplace. A Transformada de Laplace é uma técnica poderosa que converte equações diferenciais, que são comumente usadas para modelar sistemas dinâmicos no domínio do tempo, em equações algébricas no domínio da frequência. Esta conversão é extremamente útil, pois equações algébricas são tipicamente mais simples de resolver e manipular do que equações diferenciais. Além disso, ao trabalhar no domínio da frequência, torna-se mais fácil analisar como o sistema responderá a diferentes frequências de entrada, o que é essencial para entender o comportamento e a estabilidade do sistema.

As funções de transferência representam, essencialmente, como um sistema linear e invariante no tempo responde a diferentes frequências de sinais de entrada. Elas são expressas como uma razão de polinômios em termos de uma variável complexa, geralmente denotada por s (s = σ + jω, onde j é a unidade imaginária e ω é a frequência angular). Através da função de transferência, é possível determinar como o sistema amplifica ou atenua diferentes componentes de frequência de um sinal de entrada e como introduz mudanças de fase nessas componentes. Além disso, características importantes do sistema, como estabilidade, margens de ganho e fase, e resposta de frequência, podem ser extraídas diretamente da função de transferência. Essa representação é fundamental na análise e no projeto de sistemas de controle.

Pólos e zeros

Pólos e zeros são componentes críticos na função de transferência de um sistema e desempenham um papel significativo em determinar a dinâmica do sistema.

• Os zeros são os valores de s para o qual a função de transferência do sistema tende a zero. Ou seja, são as raízes do polinômio do numerador da função de transferência.
• Os pólos são os valores de s para o qual a função de transferência do sistema tende ao infinito. Isso significa que tratam-se das raízes do polinômio do denominador da função de transferência.

Considere o exemplo abaixo:

$$G_h(s) = \frac{(s+3)}{(s+1)(s+2)(s+4)}$$

Nesse caso, pode-se dizer que:

• $s = -3$ é o zero do sistema;
• $s = -1$, $s = -2$ e $s=-4$ são os pólos do sistema

A partir da determinação dos pólos e zeros de um sistema, pode-se determinar o seu comportamento dinâmico.

Analisando os pólos de um sistema, conseguimos descobrir:

• Estabilidade: Se todos os pólos têm partes reais negativas, o sistema é estável. Se algum pólo tem parte real positiva, o sistema é instável. Se os pólos estão exatamente sobre o eixo imaginário, o sistema está na fronteira da estabilidade.

• Tipo de Resposta Transitória: Pólos reais indicam uma resposta exponencial, enquanto pólos complexos conjugados indicam uma resposta oscilatória. Pólos repetidos podem resultar em respostas que são mais lentas para se estabilizar.

• Velocidade de Resposta: A parte real dos pólos determina a taxa de decaimento ou crescimento da resposta. Pólos com partes reais mais negativas resultam em respostas mais rápidas, enquanto pólos com partes reais próximas de zero indicam respostas mais lentas.

• Oscilações: Se os pólos são complexos conjugados, a parte imaginária determina a frequência de oscilação da resposta transitória.

• Amortecimento: A localização dos pólos em relação ao eixo imaginário também nos dá informações sobre o amortecimento do sistema. Pólos mais próximos do eixo imaginário indicam menos amortecimento e, portanto, mais oscilação na resposta.

• Erro de Estado Estacionário: A quantidade e localização dos pólos na origem (pólos integradores) ajudam a determinar a sensibilidade do sistema a erros de estado estacionário em resposta a diferentes tipos de entradas, como degraus, rampas, etc.

• Pólos Dominantes: Em sistemas com múltiplos pólos, os pólos mais próximos do eixo imaginário geralmente dominam o comportamento transitório do sistema, enquanto os outros têm efeitos menores.

Analisando os zeros de um sistema, conseguimos descobrir:

• Resposta de Frequência: Os zeros afetam como o sistema amplifica ou atenua diferentes frequências. Zeros próximos ao eixo imaginário podem causar um pico de ressonância, amplificando certas frequências.

• Resposta Transitória: Os zeros podem afetar a forma da resposta transitória, alterando características como o sobressinal e o tempo de acomodação.

• Rejeição de Perturbações: A localização dos zeros pode ajudar a determinar como o sistema rejeita perturbações. Zeros localizados de maneira a cancelar os efeitos de pólos indesejados podem melhorar a rejeição de perturbações.

• Atenuação de Oscilações: Zeros com partes reais negativas podem ajudar a atenuar oscilações indesejadas na resposta do sistema.

• Mudanças de Fase: Os zeros introduzem mudanças de fase no sinal de saída em relação ao sinal de entrada. Isso é importante em aplicações onde a fase do sinal é crítica, como em sistemas de comunicação.

• Tipo de Resposta: Zeros reais resultam em componentes exponenciais na resposta, enquanto zeros complexos conjugados resultam em componentes oscilatórias.

• Estabilidade Relativa: Zeros próximos aos pólos de um sistema podem indicar uma baixa margem de estabilidade, o que é importante na análise de robustez do sistema.

• Limitações de Desempenho: A presença de zeros não mínimos (zeros com partes reais positivas) pode impor limitações no desempenho do sistema, como limitar a velocidade de resposta ou de rastreamento.

• Sensibilidade a Ruídos: A localização dos zeros pode afetar a sensibilidade do sistema a ruídos e perturbações na entrada.

Resposta temporal de sistemas dinâmicos

Autoestudo

A análise da resposta temporal de um sistema de controle a sinais de entrada conhecidos, como degraus, impulso, rampa, entre outros, é fundamental para avaliar o desempenho do sistema e para o projeto de controladores. Através desta análise, é possível extrair parâmetros importantes como o tempo de subida, tempo de acomodação, sobressinal e erro de estado estacionário, que são críticos para entender como o sistema reage a mudanças ou perturbações. Além disso, a resposta temporal fornece insights sobre a estabilidade do sistema, pois um sistema instável pode ter uma resposta que diverge com o tempo. Observar como o sistema responde a um degrau, por exemplo, pode ser especialmente útil, pois este tipo de entrada é frequentemente usado para representar mudanças súbitas ou comandos de referência em aplicações práticas.

Além disso, a análise de resposta temporal é essencial para a identificação de sistemas. A identificação de sistemas envolve a construção de um modelo matemático que representa o comportamento de um sistema real com base em dados de entrada e saída. Ao aplicar sinais conhecidos ao sistema e medir suas respostas, é possível estimar os parâmetros do modelo. Isso é particularmente útil quando se trata de sistemas complexos ou de difícil modelagem teórica. Com um modelo preciso em mãos, os engenheiros podem realizar simulações, análise de sensibilidade e projetar controladores que atendam às especificações de desempenho, garantindo assim um comportamento adequado e seguro do sistema de controle em operação real.

Resposta padrão de um sistema de segunda ordem

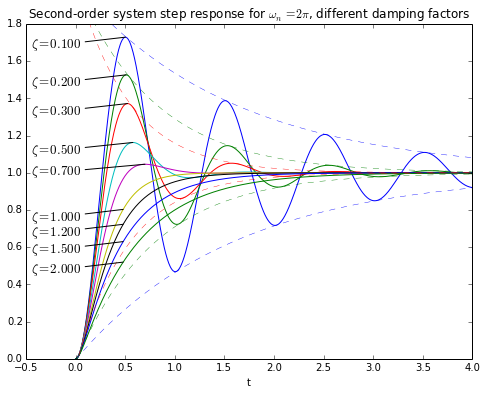
O sistema genérico de segunda ordem desempenha um papel fundamental na análise e simplificação de sistemas de controle, pois muitos sistemas reais podem ser aproximados ou representados por um modelo de segunda ordem. Esse modelo, geralmente descrito por uma equação diferencial de segunda ordem ou uma função de transferência com dois pólos, é caracterizado por três parâmetros principais: ganho, frequência natural e razão de amortecimento. O uso de um sistema de segunda ordem simplifica significativamente a análise, pois a resposta temporal desse tipo de sistema é bem compreendida e pode ser descrita por um conjunto de expressões padrão. Além disso, um sistema de segunda ordem captura comportamentos dinâmicos importantes, como oscilações e amortecimento, que são comuns em muitos sistemas reais. Ao aproximar sistemas de ordem superior como sistemas de segunda ordem, os engenheiros podem obter insights valiosos sobre o comportamento do sistema e tomar decisões de projeto de forma mais eficiente e intuitiva.

A equação de um sistema genérico de segunda ordem é:

$$G(s) = \frac{\omega_n^2}{s^2+\zeta\omega_ns+\omega_n^2}$$

Onde:

• $\omega_n$ representa a frequência natural do sistema; e
• $\zeta$ representa o coeficiente de amortecimento do sistema.

A imagem a seguir representa a influência do coeficiente de amortecimento de um sistema em sua resposta dinâmica. É possível ver também a correlação de cada um dos sistemas com seus pólos e zeros.

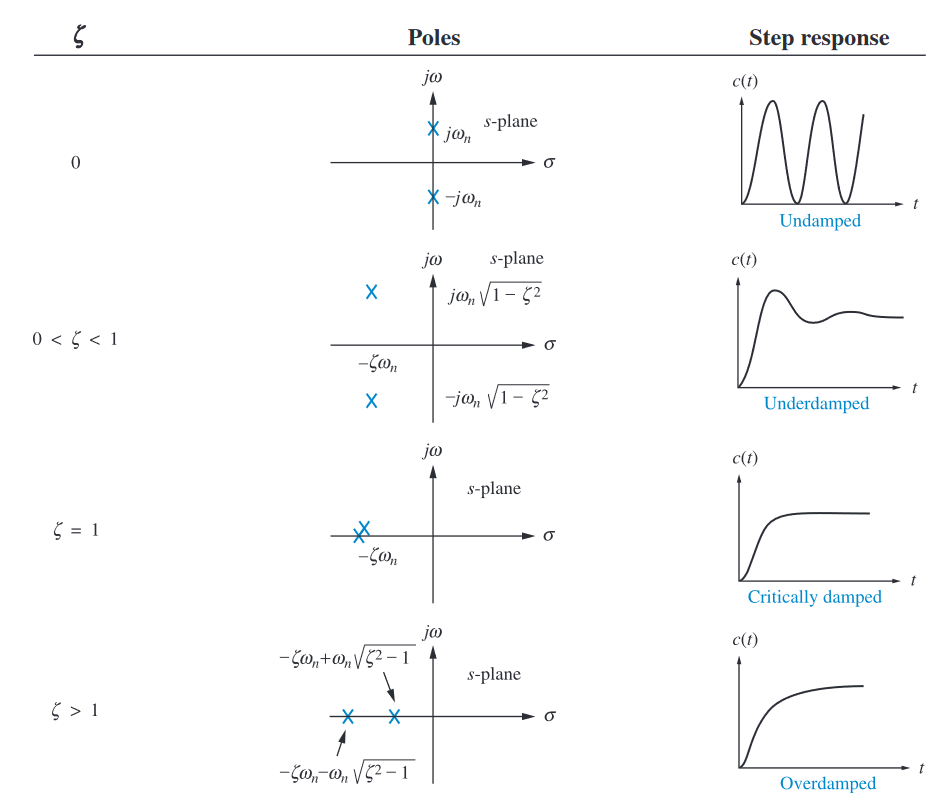
Considere a resposta de um sistema de segunda ordem a um degrau:

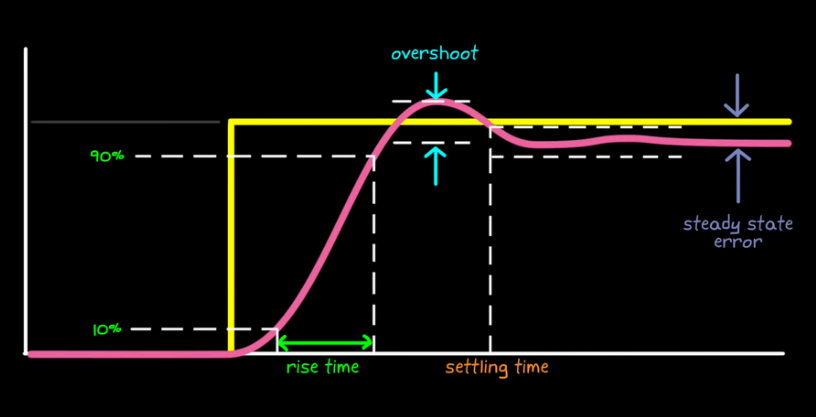
A partir de análise gráfica ou da equação do sistema de segunda ordem, podemos extrair as seguintes informações relevantes:

• Máximo sobressinal (overshoot):

$$M_p=\frac{-\zeta\pi}{e^{\sqrt{1-\zeta^2}}}$$

• Tempo de pico (instante no qual o sinal atinge o seu ponto de máximo):

$$t_p = \frac{\pi}{\omega_n\sqrt{1-\zeta^2}}$$

• Tempo de assentamento (settling time):

$$t_s = \frac{4}{\zeta\omega_n}$$

• Período da função: tempo necessário para que o sinal chegue a $63,5\%$ da referência (degrau)

• Tempo de subida: tempo necessário para que o sinal saída de $10\%$ a $90\%$ do sinal de referência (degrau).